Conical Flow Diagram
This notebook shows how to visualize the Taylor-Maccoll equation for conical flow.
Given the nondimensional velocity \(V^{'}\):
\[V^{'} = \frac{V}{V_{max}}\]
the Taylor-Maccoll equation is:
\[\begin{split}\begin{equation}
\begin{aligned}
\frac{\gamma - 1}{2} &\left[ 1 - V^{'2}_{r} - \left(\frac{d V^{'}_{r}}{d \theta}\right)^{2} \right] \left[ 2 V^{'}_{r} + \frac{d V^{'}_{r}}{d \theta} \cot{\theta} + \frac{d^{2} V^{'}_{r}}{d \theta^{2}} \right] \\
& - \frac{d V^{'}_{r}}{d \theta} \left[ V^{'}_{r} \frac{d V^{'}_{r}}{d \theta} + \frac{d V^{'}_{r}}{d \theta} \frac{d^{2} V^{'}_{r}}{d \theta^{2}} \right] = 0
\end{aligned}
\end{equation}\end{split}\]
where \(V^{'}_{r}\) is the nondimensional velocity component along a ray starting at the tip of the cone.
[1]:
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import matplotlib.cm as cmx
from pygasflow.shockwave import (
mach_cone_angle_from_shock_angle,
max_theta_c_from_mach,
beta_theta_c_for_unit_mach_downstream,
load_data
)
import numpy as np
To generate the Mach curves we will use the mach_cone_angle_from_shock_angle function:
[2]:
help(mach_cone_angle_from_shock_angle)
Help on function mach_cone_angle_from_shock_angle in module pygasflow.shockwave:
mach_cone_angle_from_shock_angle(M, beta, gamma=1.4)
Compute the half-cone angle and the Mach number at the surface of the cone.
NOTE: this function is undecorated, hence no check is performed to assure
the validity of the input parameters. It's up to the user to assure that.
Parameters
----------
M : float
Upstream Mach number. Must be > 1.
beta : float
Shock Angle in degrees. Must be mach_angle <= beta <= 90.
NOTE: no check is done over beta. If an error is raised during the
computation, make sure beta is at least ever so slightly bigger than
the mach angle.
gamma : float, optional
Specific heats ratio. Default to 1.4. Must be > 1.
Returns
-------
Mc : float
Mach number at the surface of the cone
theta_c : float
Half-cone angle in degrees.
Essentialy, we create an array containing the interested Mach numbers and we will loop over it, integrating the Taylor-Maccoll equation for the specified parameters.
[3]:
Minf = [1.05, 1.2, 1.5, 2, 5, 10000]
gamma = 1.4
N = 200
# colors
jet = plt.get_cmap('hsv')
cNorm = colors.Normalize(vmin=0, vmax=len(Minf))
scalarMap = cmx.ScalarMappable(norm=cNorm, cmap=jet)
c = [scalarMap.to_rgba(i) for i in range(len(Minf))]
# labels
lbls = [r"$M_{1}$ = " + str(Minf[i]) for i in range(len(Minf))]
lbls[-1] = r"$M_1$ = $\infty$"
plt.figure()
for j, M in enumerate(Minf):
theta_c = np.zeros(N)
# NOTE: to avoid errors in the integration process of Taylor-Maccoll equation,
# beta should be different than Mach angle and 90deg, hence an offset is applied.
offset = 1e-08
theta_s = np.linspace(np.rad2deg(np.arcsin(1 / M)) + offset, 90 - offset, N)
for i, ts in enumerate(theta_s):
Mc, tc = mach_cone_angle_from_shock_angle(M, ts, gamma)
theta_c[i] = tc
theta_c = np.insert(theta_c, 0, 0)
theta_c = np.append(theta_c, 0)
theta_s = np.insert(theta_s, 0, np.rad2deg(np.arcsin(1 / M)))
theta_s = np.append(theta_s, 90)
plt.plot(theta_c, theta_s, color=c[j], label=lbls[j])
# Compute the line passing through theta_c_max
M = np.asarray([1.0005, 1.0025, 1.005, 1.025, 1.05, 1.07, 1.09,
1.12, 1.15, 1.2, 1.25, 1.3, 1.35, 1.4, 1.45, 1.5,
1.6, 1.75, 2, 2.25, 3, 4, 5, 10, 100, 10000])
b = np.zeros_like(M)
tc = np.zeros_like(M)
for i, m in enumerate(M):
_, tc[i], b[i] = max_theta_c_from_mach(m, gamma)
tc = np.insert(tc, 0, 0)
b = np.insert(b, 0, 90)
plt.plot(tc, b, '--', color="0.2", linewidth=1)
# select an index where to put the annotation (chosen by trial and error)
i = 16
plt.annotate("strong",
(tc[i], b[i]),
(tc[i], b[i] + 10),
horizontalalignment='center',
arrowprops=dict(arrowstyle = "<-")
)
plt.annotate("weak",
(tc[i], b[i]),
(tc[i], b[i] - 10),
horizontalalignment='center',
arrowprops=dict(arrowstyle = "<-"),
)
M, beta, theta_c = load_data(gamma)
plt.plot(np.asarray(theta_c), np.asarray(beta), ':', color="0.2", linewidth=1)
i = 54
plt.annotate("$M_{2} < 1$",
(theta_c[i], beta[i]),
(theta_c[i], beta[i] + 10),
horizontalalignment='center',
arrowprops=dict(arrowstyle = "<-", color="0.3"),
color="0.3",
)
plt.annotate("$M_{2} > 1$",
(theta_c[i], beta[i]),
(theta_c[i], beta[i] - 10),
horizontalalignment='center',
arrowprops=dict(arrowstyle = "<-", color="0.3"),
color="0.3",
)
# If there is no data for M2=1, we just need to generate it. IT IS SLOW!!!
# M = np.asarray([1.05, 1.2, 1.35, 1.5, 2, 3, 5, 10000])
# beta = np.zeros_like(M)
# theta_c = np.zeros_like(M)
# for i, m in enumerate(M):
# beta[i], theta_c[i] = beta_theta_c_for_unit_mach_downstream(m, gamma)
# theta_c = np.insert(theta_c, 0, 0)
# beta = np.insert(beta, 0, 90)
# plt.plot(theta_c, beta, ':', color="0.2", linewidth=1)
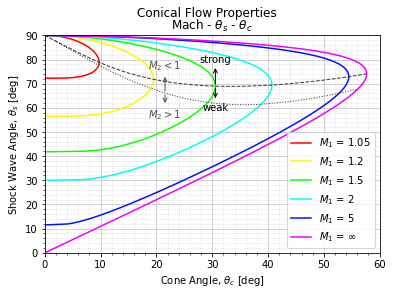
plt.suptitle("Conical Flow Properties")
plt.title(r"Mach - $\theta_{s}$ - $\theta_{c}$")
plt.xlabel(r"Cone Angle, $\theta_{c}$ [deg]")
plt.ylabel(r"Shock Wave Angle, $\theta_{s}$ [deg]")
plt.xlim((0, 60))
plt.ylim((0, 90))
plt.minorticks_on()
plt.grid(which='major', linestyle='-', alpha=0.7)
plt.grid(which='minor', linestyle=':', alpha=0.5)
plt.legend(loc="lower right")
plt.show()
[ ]: